Interaction of 𝛾-radiation and matter
When 𝛾-rays penetrate matter, they can interact with atoms of the medium in various ways. The three main interaction processes in the relevant energy range of the g-ray studies of natural radioactivity, 10keV<Eg<3MeV, are 1) photo-electric absorption, 2) Compton scattering and 3) pair-production. This chapter will describe what the effect of these interaction processes is on the g-ray spectrum of a source with mono-energetic photons (see e.g. Debertin and Helmer, 1988; Knoll, 1979).
In the photo-electric absorption process, the full photon energy is absorbed and transferred to a so-called photo-electron. This electron is ejected from the atom with an energy Ee equal to:
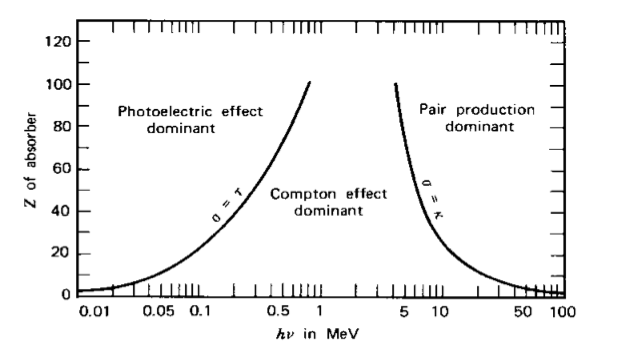
where E𝛾 is the energy of the incident 𝛾-ray and Eb the binding energy of the electron in its original shell. Unless the interaction occurs in a vacuum, the ejected electron will be slowed down in the neighbouring material and its energy will be absorbed. The photo-electric effect is the predominant mode of interaction of gamma rays of relatively low energies. Besides the energy of the gamma rays, also the atomic number, Z, of the material determines the probability that a gamma ray will interact. This probability is expressed in cross-section (τ) per unit mass. This cross-section cannot be described by a single analytical expression, but its dependence on the atomic number and energy can be approximately described by:
where the exponent n ranges between 3 and 4. The strong Z dependence indicates that a high Z material is very effective in the absorption of photons. The strong dependence on the photon energy, is the reason why this effect is the dominant mode of interaction at low energies (<0.5 MeV). The photo-electric absorption effect in a detector will result in a sharp peak, the so-called photo peak. The intensity of the peak is a function of the intensity of the 𝛾-ray flux and the absorption properties of the material.
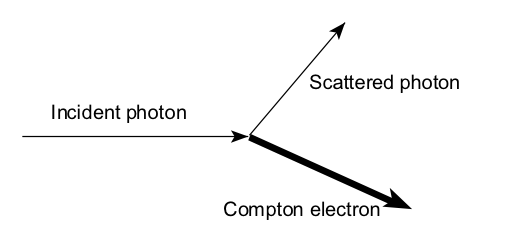
In the Compton scattering process, only a portion of the photon energy is transferred to a “Compton electron” and the remainder is carried away by a secondary photon (Eg’). The energies of the outgoing electron and secondary photon are related to the scattering angle. After scattering, the secondary photon can be absorbed by photo-electric absorption or scattered again by the Compton scattering process. It is possible that the photon or electron scatters out of the medium without depositing its full energy. The cross-section for Compton scattering (σ) per unit mass can be approximated by:
The fact that the Compton cross-section is independent of the atomic number Z, indicates that, contrary to the photo-electric effect, Compton scattering is more or less independent of the medium. The inverse relation with the photons energy indicates that Compton scattering is dominant at higher energies (~0.5-5 MeV).
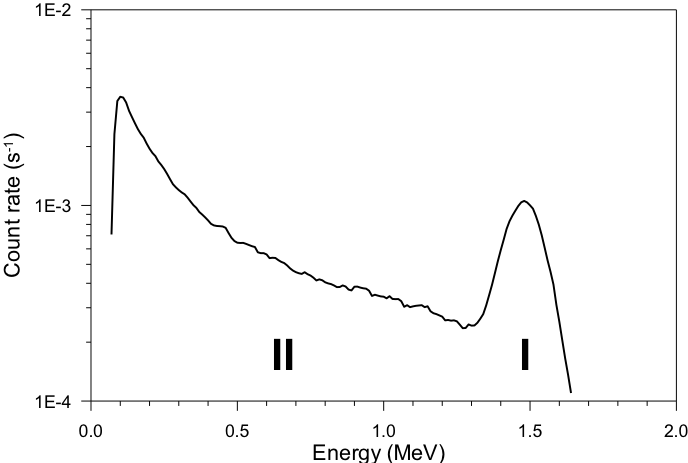
In an energy spectrum of a mono-energetic g-ray bundle, the scattering process will lead to a distribution of energies lower than the energy of the incident g-ray: the Compton continuum is composed of a photopeak, due to the photo-electric absorption and of Compton scattered events in the detector (releasing their full energy by multiple scattering), and a continuum. This continuum is composed of Compton scattered photons that are not completely collected in the detector and of photons that were Compton scattered in the surrounding medium, and entered the detector as scattered photons with a lower energy than the original photon.
In the process of pair production, a photon is converted to an electron-positron pair, the electron is slowed down in the surrounding matter and, the positron annihilates with electrons in the matter. The threshold for pair production is 1.022 MeV, but becomes dominant in the energy range >4 MeV. The cross-section of pair production depends on Z2 and increases sharply with the photon energy. Since the maximum energy of natural 𝛾-rays is 2.6 MeV, this process is not of great importance and will therefore not be considered in further discussion.
Attenuation of 𝛾-rays
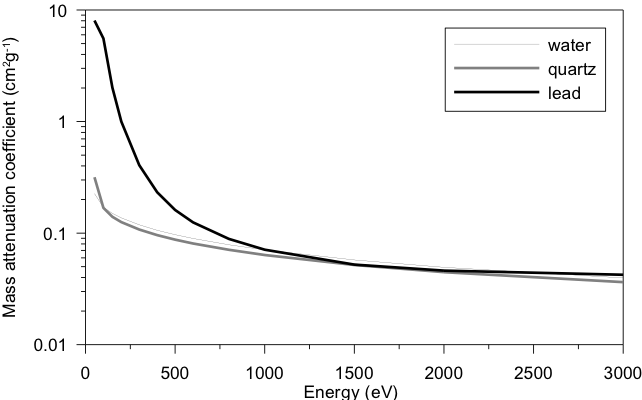
If a parallel beam of mono-energetic photons passes through an absorber with thickness z, density r and effective atomic number Zeff, photons will loose energy due to interaction processes. The probability per unit path length that a photon or 𝛾-quant is removed from the beam depends on the energy of the 𝛾-quant (E𝛾), the density and effective atomic number of the medium and is described by m: the linear attenuation coefficient. The linear attenuation coefficient (µ) has the dimension m-1 and varies with the density 𝜌 of the absorber. Alternatively, the linear attenuation coefficient µ, can be replaced by the mass-attenuation coefficient µ’ (defined µ’=µ𝜌-1), with the dimension kg-1m2. The mass-attenuation coefficient is more or less material unspecific (Sowa et al., 1989), does not depend on the density of a material and is therefore independent on the state of a material (e.g. in liquid or in gaseous form) or on the packing of the material.
Since both the photo-electric effect and Compton scattering remove photons from the beam, the total mass-attenuation coefficient is the sum of the two cross-sections:
In the energy range of interest the attenuation coefficient decreases with increasing photon energy, which means that high energy photons have a larger possibility to pass an absorber undisturbed than low energy photons.
The number of photons N(E𝛾) of one particular energy E𝛾 that pass undisturbed through the absorber with thickness z, is given by:
where N0(E𝛾) is the initial number of photons of energy E𝛾 hitting the absorber.
When sediments or soils are considered, the medium consists of a mixture of elements. The mass-attenuation coefficient for a mixture of elements can be obtained by:
where mi is the fraction (by mass) of element i (with mass-attenuation coefficient mi’) in the mixture.
In the case of a point source and an absorber in front of a detector, part of the Compton energies in the spectrum originate from the Compton-scattered g-rays in the detector itself. Also 𝛾-rays that are Compton-scattered within the absorber will reach the detector where they are detected by Compton scattering or photo-electric-effect. Also photons that enter the detector via back-scattering in the surrounding medium, will end in the Compton continuum (part II in the figure above). These additional photons contribute to the shape and intensity of the spectrum. This effect is called build-up.
